详解MegatronLM Tensor模型并行训练(Tensor Parallel)

发表于 分类于 本文字数： 2k 阅读时长 ≈ 7 分钟

1. 背景介绍

MegatronLM的第一篇论文【Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism】是2020年出的，针对billion级别的模型进行训练，例如具有38亿参数的类GPT-2的transformer模型和具有39亿参数的BERT模型。

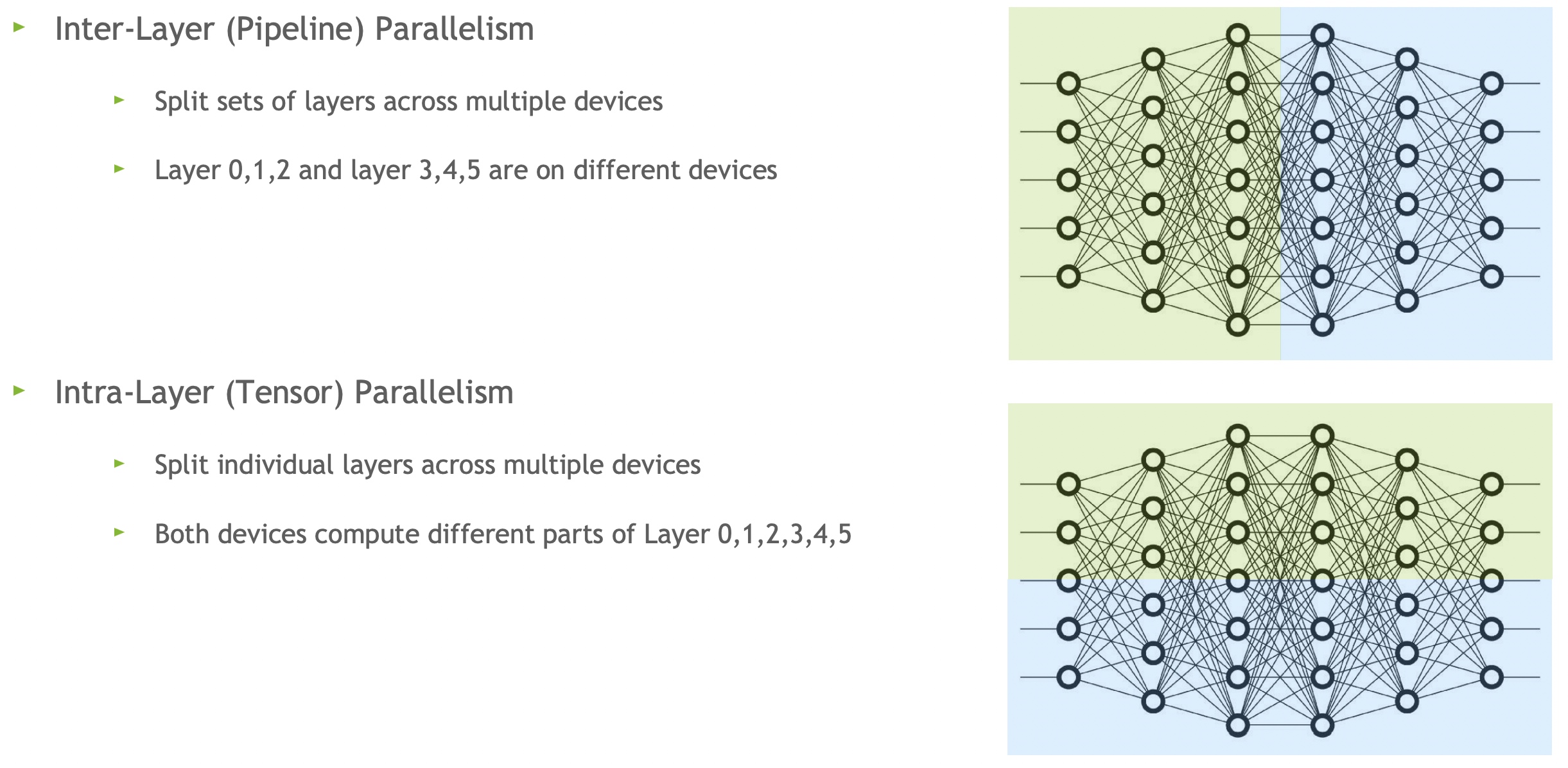
分布式训练的模型并行有两种方式，一种是层间并行(inter-layer)，也就是Pipeline流水线并行，相当于下图对整个模型竖切后每个device各保存3个layer(0,1,2和3,4,5)；一种是层内并行(intra-layer)的方式进行，也就是Tensor模型并行，相当于下图横切后每个device各保留6个layer的一半。

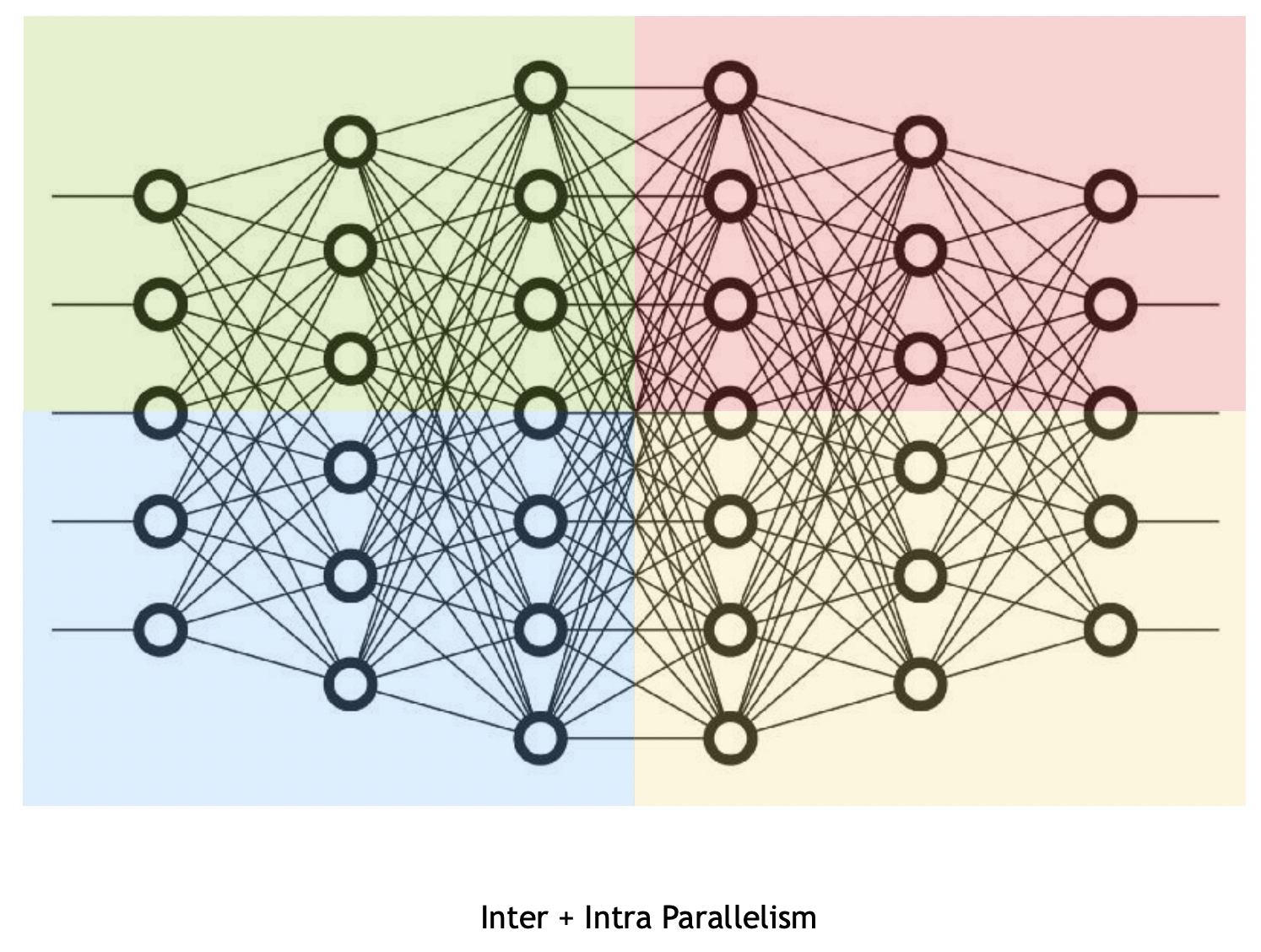
在实际中由于Pipeline并行和Tensor并行是正交的，所以可以同时使用，如下图pipeline并行是竖切，tensor并行是横切，每个色块代表一个device，一个模型运行在4个device上。

接下来重点来看Megatron Tensor并行在transformer模型上的实现。

2. 详细介绍

2.1 Tensor并行计算方法介绍

Tensor计算要进行并行计算，主要方法是通过合理的方式对输入矩阵和参数矩阵进行分块，然后对不同分块分别进行计算。

2.1.1 对参数weight矩阵进行横切(Row Parallel Linear Layer)

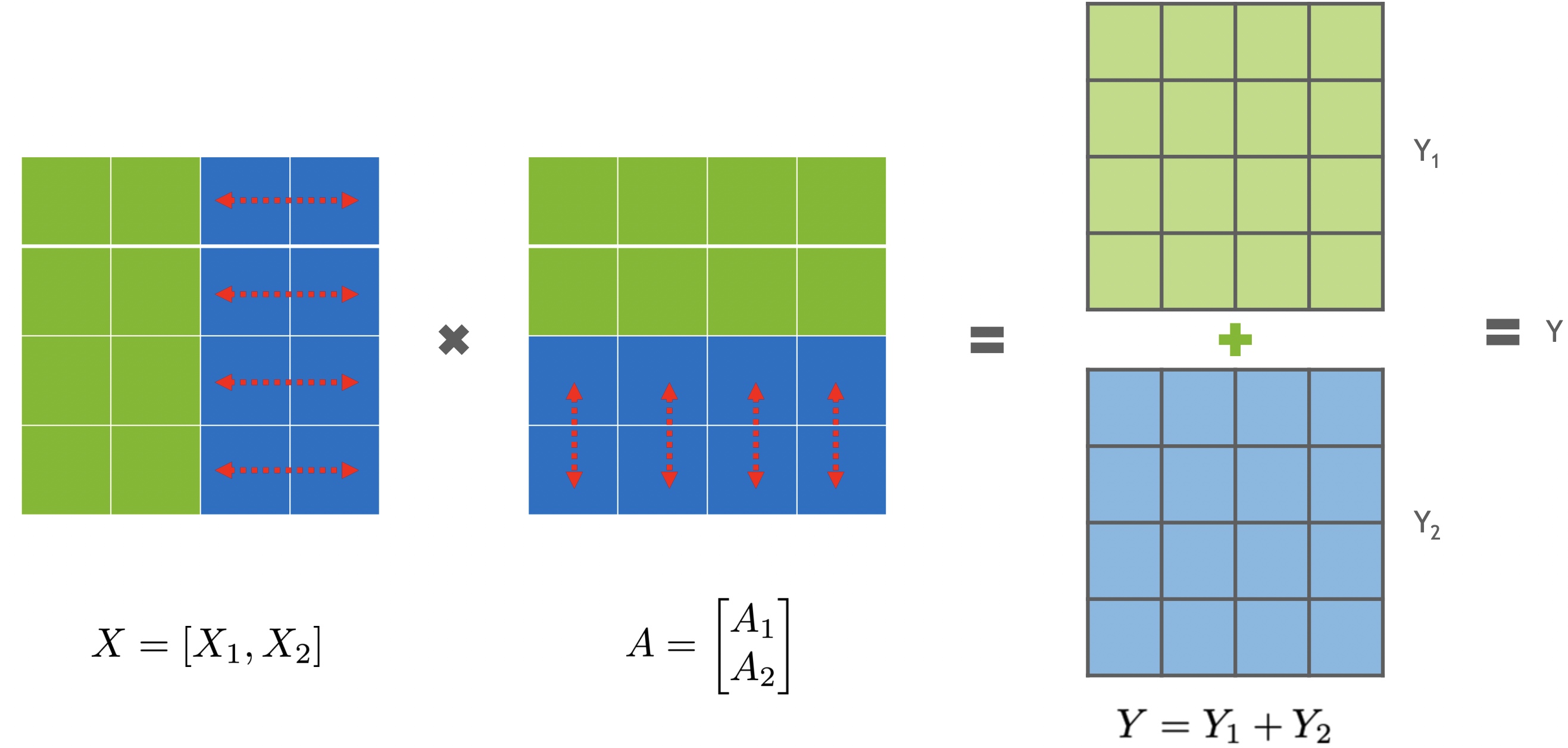
以下图为例，\(X\) 看成是输入矩阵，\(A\) 看成是参数weight矩阵，这里是对 \(A\) 横向切分成两个小的矩阵 \(A_1\) 和 \(A_2\) ，然后为了相乘对应 \(X\) 也切分为 \(X_1\) 和 \(X_2\)。

\[\begin{gather*} \begin{aligned} X \times A &= \left[ X_1 \ X_2\right] \times \left[ {}^{A_1}_{A_2} \right] \\ &= X_1 \cdot A_1 + X_2 \cdot A_2 \end{aligned} \end{gather*}\]

假设 \(X\) 的shape大小是 \((100， 300)\), \(X1、X2\) 的shape大小都是 \((100, 150)\)；\(A\) 的shape大小是 \((300, 200)\)； \(A1、A2\) 的shape大小是 \((150, 200)\)；\(Y_1、Y_2\) 的shape大小是 \((100, 200)\) , 其中 \(Y_1=X_1 \cdot A_1\) 以及 \(Y_2=X_2 \cdot A_2\)；\(Y\) 的shape大小是\((100, 200)\)。

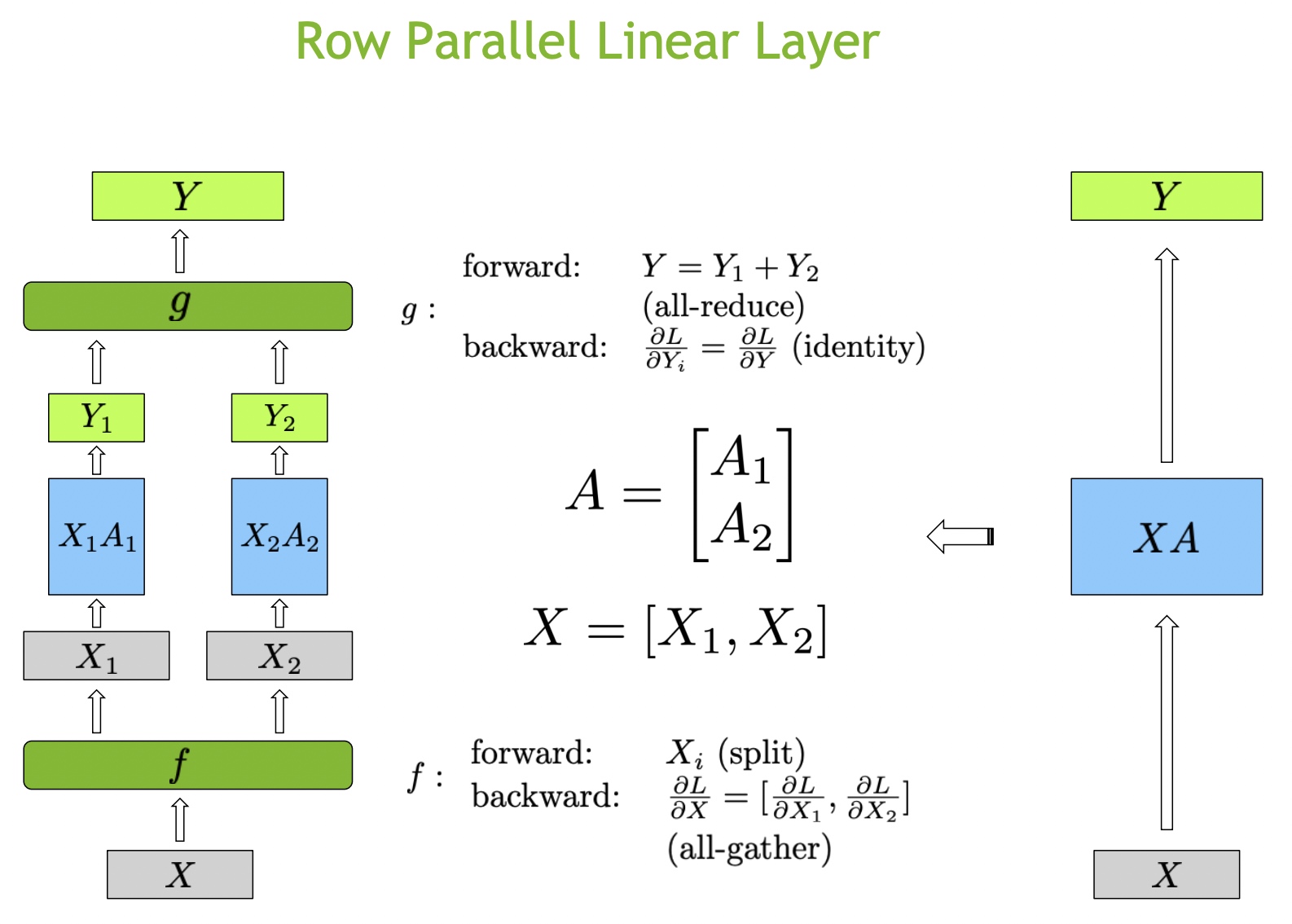
从前后向的角度来看按行切分 \(A\) 参数矩阵的过程，\(f\) 函数前向会对 \(X\) 输入进行切分两份 \(X_1, X_2\)，在反向会对回传的梯度通过all-gather方法进行拼接；分开计算完有两部分结果需要合并相加成最终的结果，所以在后面有一个 \(g\) 函数前向过程会通过all-reduce方法对结果进行累加，在反向的时候会分别求梯度(也就是identity)。

2.1.2 对参数矩阵进行纵切(Column Parallel Linear Layer)

以下图为例，\(X\) 看成是输入矩阵，\(A\) 看成是参数weight矩阵，这里是对 \(A\) 纵向切分成两个小的矩阵 \(A_1\) 和 \(A_2\) ，\(X\) 是整个参与计算。

\[\begin{gather*} \begin{aligned} X \times A &= X \times \left[ {A_1}, \ {A_2} \right] \\ &= \left[ X \cdot A_1,\ X \cdot A_2 \right] \end{aligned} \end{gather*}\]

假设 \(X\) 的shape大小是 \((100， 300)\)；\(A\) 的shape大小是 \((300, 200)\)； \(A1、A2\) 的shape大小是 \((300, 100)\)；\(Y_1、Y_2\) 的shape大小是 \((100, 100)\) , 其中 \(Y_1=X \cdot A_1\) 以及 \(Y_2=X \cdot A_2\); \(Y\) 的shape大小是 \((100, 200)\)。

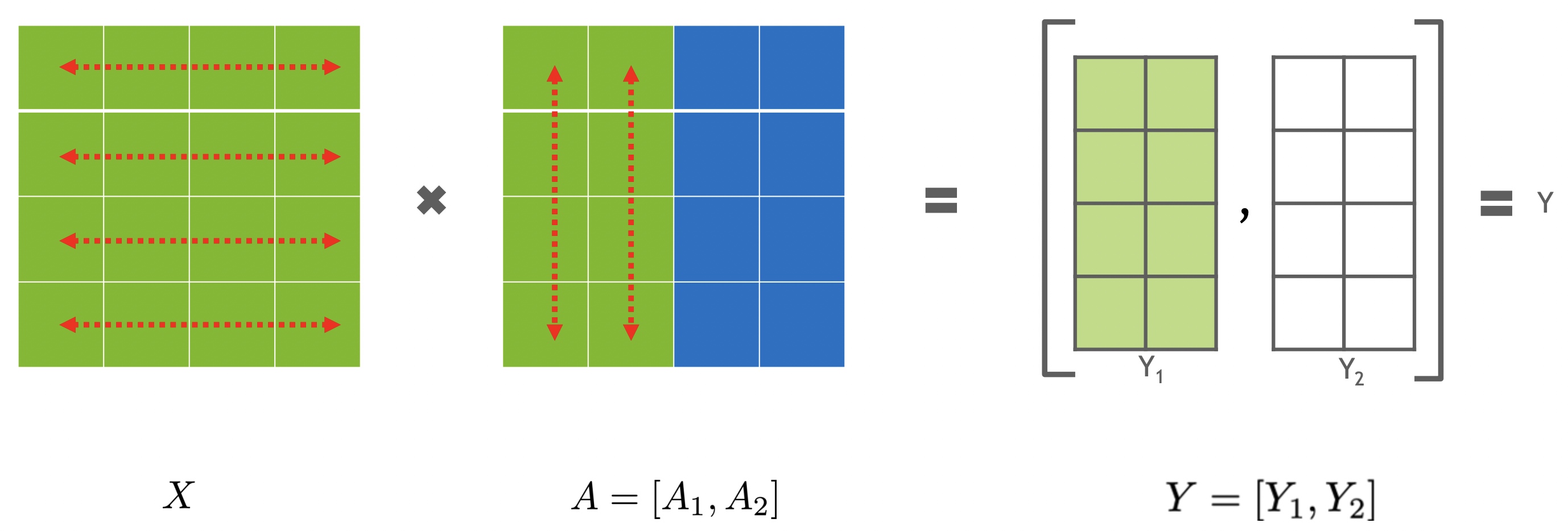
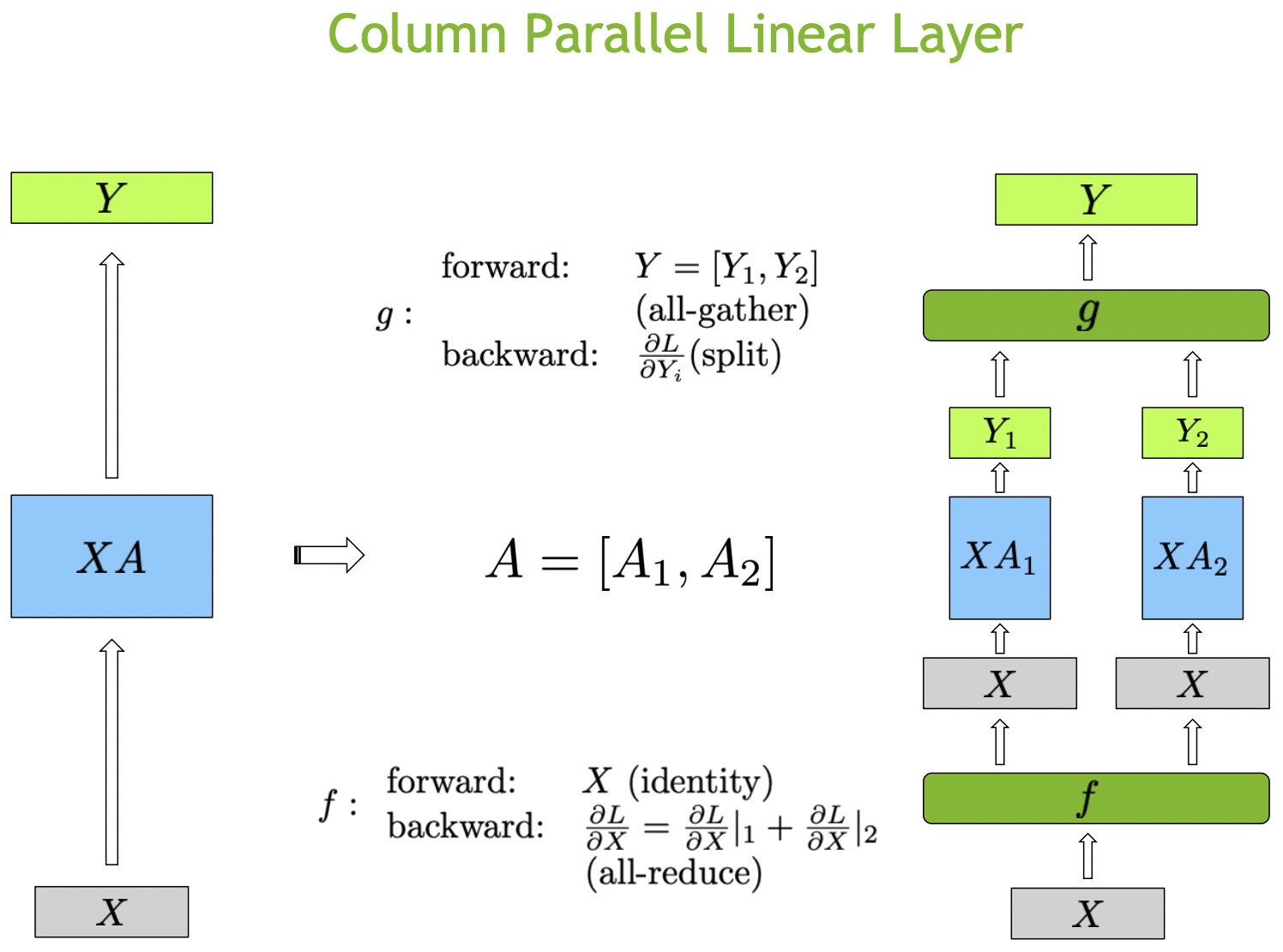
从前后向的角度来看按列切分 \(A\) 参数矩阵的过程，\(f\) 函数前向会重复使用输入 \(X\) 进行两部分的计算(identity)；在反向会对回传的梯度通过all-reduce方法进行累加；分开计算完有两部分结果需要拼接成最终的结果，所以在后面有一个 \(g\) 函数前向过程会通过all-gather方法对结果进行拼接，在反向的时候会对梯度矩阵进行split成两部分，再往后回传。

2.2 Tensor并行在GPT Transformer中的应用

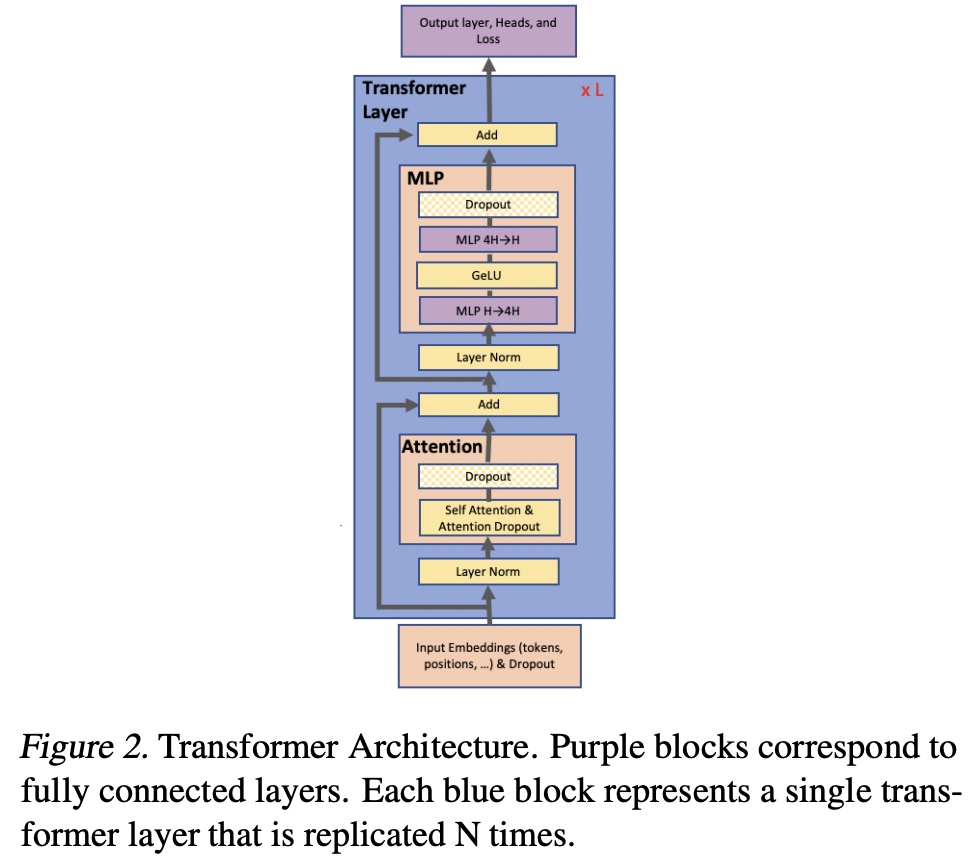
2.2.1 GPT Transformer结构

在GPT Transformer结构中是由一个Attention模块和MLP模块组成。在Attention模块中先是有self-attention层加上dropout组成；在MLP模块有两个MLP层，第一个MLP把维度从H变为4H，第二个MLP把维度从4H变回H，中间是采用了非线性的激活GeLU；每层的连接上也使用了像Resnet的残差连接。。

2.2.2 对MLP模块进行Tensor并行

在进行Tensor并行过程中，要选择哪种方式来对MLP模块中的矩阵进行切分？

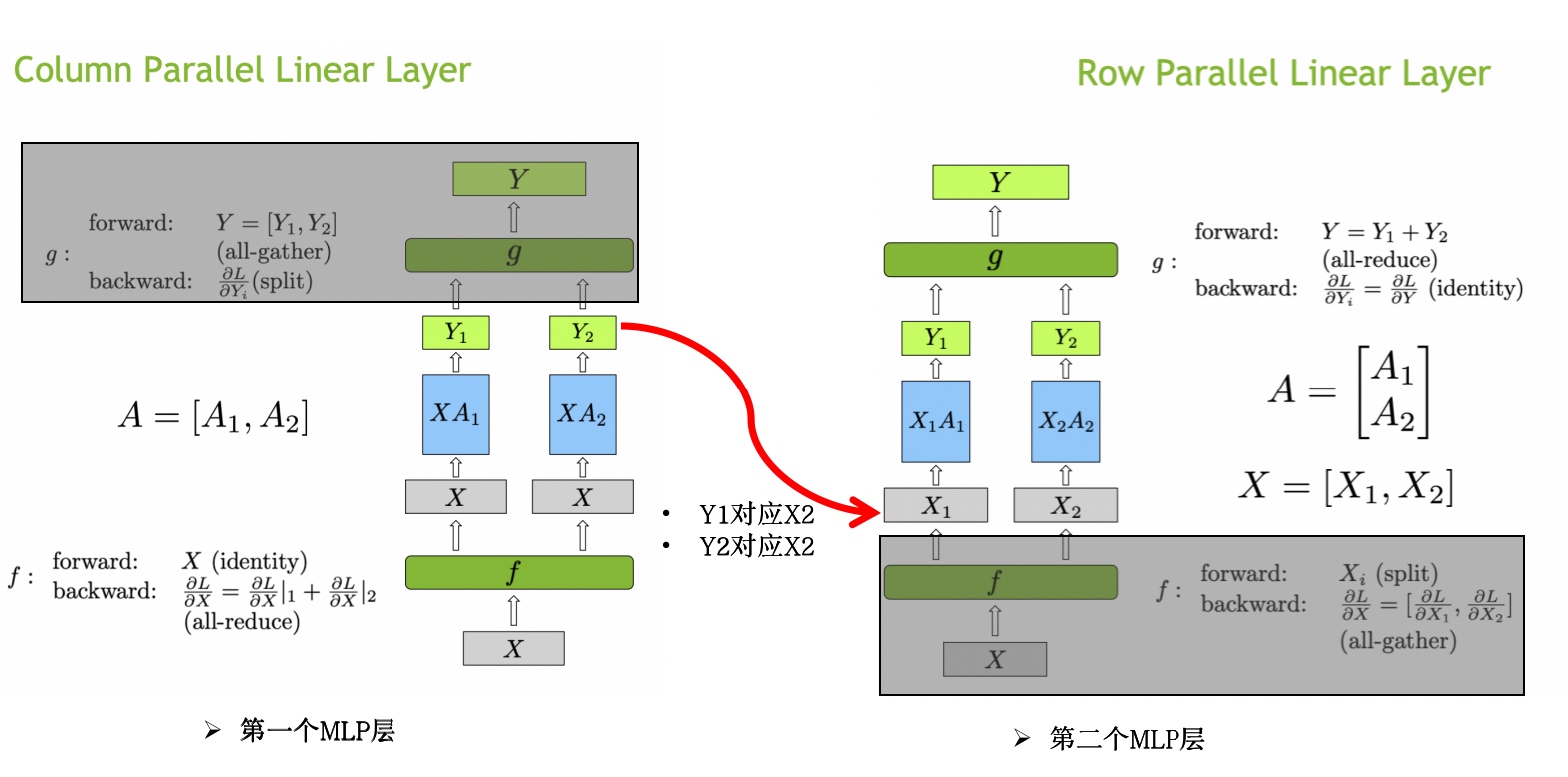
先看MLP模块中的第一个MLP层，对应的计算操作可以表达成 \(Y=GeLU(XA)\)。如果对 \(A\) 按行(Row)进行横向切分的话，\(X=\left[ X_1, X_2\right], A=\left[ {}^{A_1}_{A_2} \right], Y=GeLU(X_1 A_1 + X_2 A_2)\), 由于GeLU不是线性的不好进行后续的并行【\(GeLU(X_1 A_1 + X_2 A_2) \neq GeLU(X_1 A_1) + GeLU(X_2 A_2)\)】, 所以不采用按行的Tensor切分方式。所以要采用对每一个MLP层的 \(A\) 按列(Column)进行纵向切分的方式，对应 \(A=\left[ A_1, A_2 \right], Y=\left[ Y_1, Y_2 \right]=\left[ GeLU(X A_1), GeLU(X A_2) \right]\)。

再来看MLP模块中的第二个MLP层，在第一个MLP层在做完GeLU操作后是有两部分结果，还需要\(g\)函数进行合并操作，但是可以和第二个MLP层一起计算，这样第一个MLP层的 \(g\) 函数和第二个MLP层的 \(f\) 函数都可以去掉；对于第二个MLP层没有GeLU操作，要采用对 \(A\) 按行(Row)进行横向切分才能接上第一个MLP层。如下图阴影部分是去掉的部分，对应公式如下：

\[\begin{gather*} \begin{aligned} \\ A^{(1)} &=\left[ A^{(1)}_1, A^{(1)}_2 \right] \\ Y^{(1)}_1 &= GeLU(X A^{(1)}_1) \\ Y^{(1)}_2 &= GeLU(X A^{(1)}_2) \\ Y^{(1)} &=\left[ Y^{(1)}_1, Y^{(1)}_2 \right] \\ &=\left[ GeLU(X A^{(1)}_1), GeLU(X A^{(1)}_2) \right] \\ \\ A^{(2)} &= \left[ {}^{A^{(2)}_1}_{A^{(2)}_2} \right] \\ Y^{(1)} \times A^{(2)} &= \left[ Y^{(1)}_1 \ Y^{(1)}_2\right] \times \left[ {}^{A^{(2)}_1}_{A^{(2)}_2} \right] \\ &= \left[ Y^{(1)}_1 \cdot A^{(2)}_1, Y^{(1)}_2 \cdot A^{(2)}_2 \right] \\ Y^{(2)} &= Y^{(1)}_1 \cdot A^{(2)}_1 + Y^{(1)}_2 \cdot A^{(2)}_2 \\ \\ \end{aligned} \end{gather*}\]

最终对应整体的图如下：

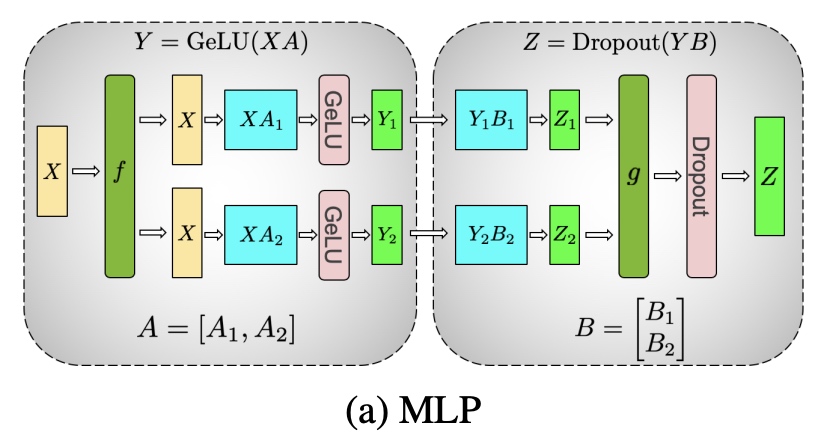
上图MLP模块中的 \(f\) 和 \(g\) 函数在PyTorch中的伪码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class f(torch.autograd.Function):
    def forward(ctx, x):
        return x
    def backward(ctx, gradient):
        all_reduce(gradient)
        return gradient

class g(torch.autograd.Function):
    def forward(ctx, x):
        all_reduce(x)
        return x
    def backward(ctx, gradient):
        return gradient

2.2.3 对Attention模块进行Tensor并行

回顾下Attention的计算过程有哪些矩阵计算, 首先是在前面\(QK/V\)计算中每个Head中\(Q/K/V\)对应有三个weight矩阵，然后是在最后对\(Z_n\) 进行汇总时要用到weight矩阵 \(W^0\)。

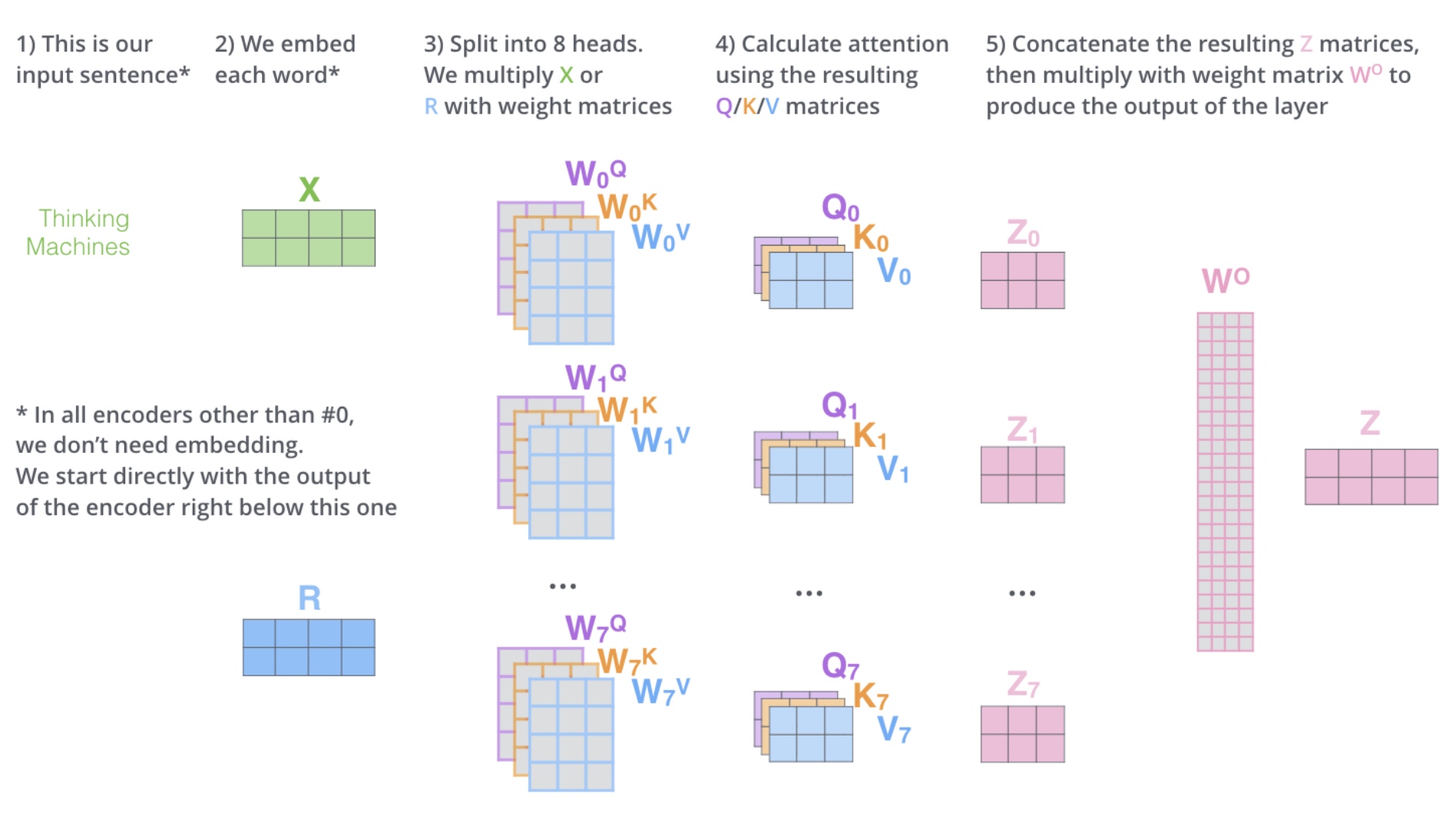
Attention模块中对Tensor并行切分方式跟MLP类似，先分别对 \(Q/K/V\)按列进行切分，计算的结果是多个独立的部分，然后对最终的weight矩阵进行按行切分，得到的结果进行累加操作(all_reduce)得到最终的结果。因为在前向输入是多次复用的，所以在反向时需要对梯度进行累加操作(all_reduce)。这样attention计算中也有两次all_reduce操作。

最终对应整体的图如下：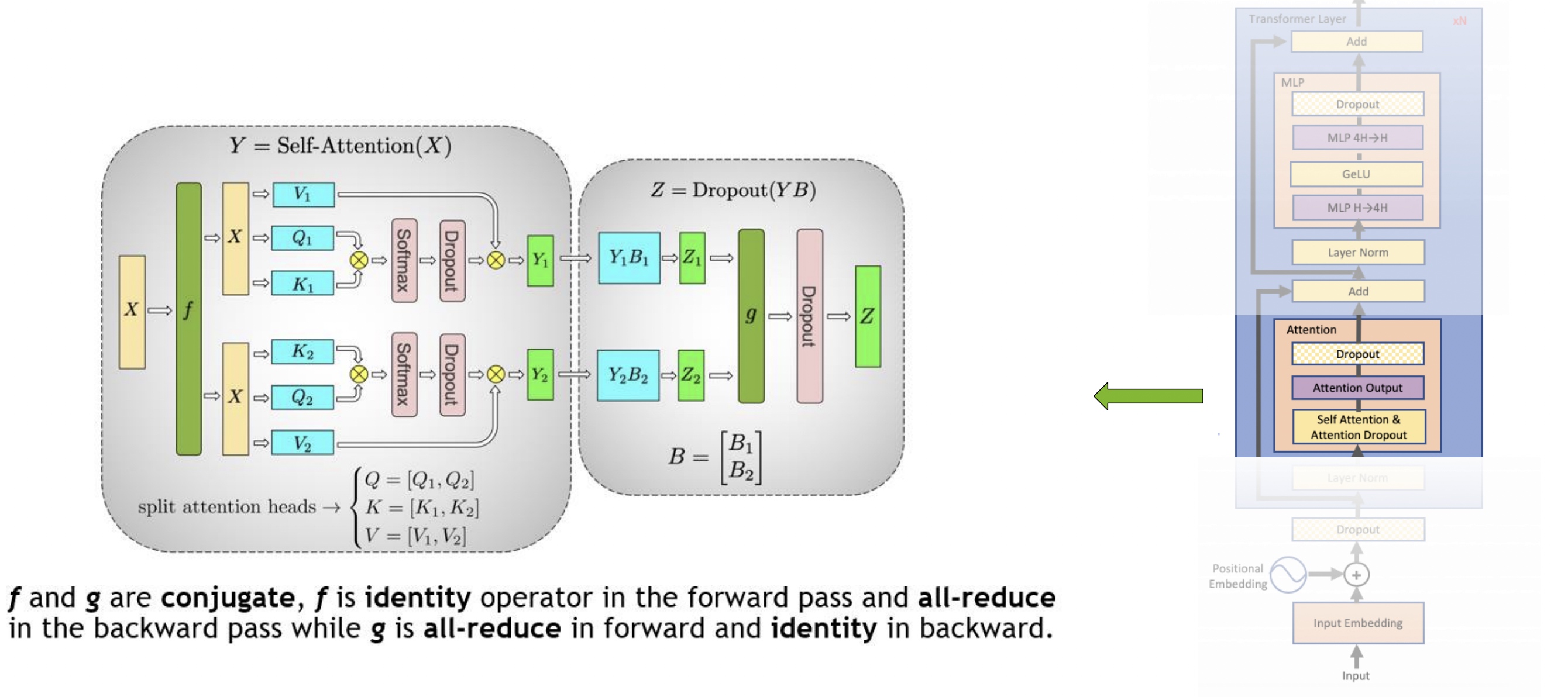

在整个Transformer结构中通信上共需要4次All-Reduce操作。

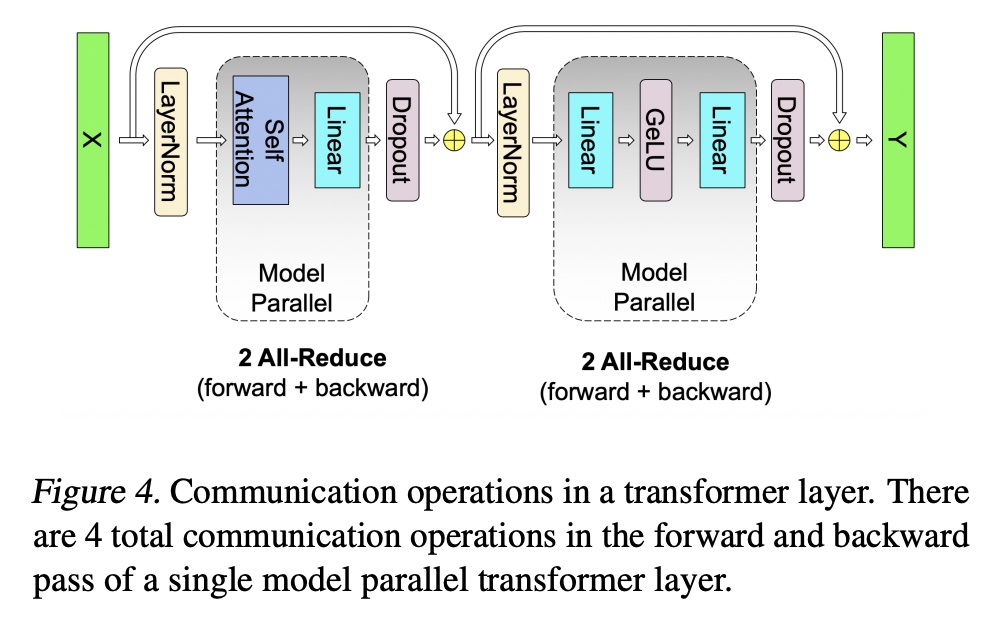
2.2.4 对输出Embedding层进行Tensor并行

以下是GPT计算的整体公式：\(W_e\)是输入的embedding层, \(W_p\)是position embedding层，\(W_e\)同时也在最终输出时复用了，embedding层的shape大小是 \({hidden-size(H) \times vocabulary-size(v)}\) 。

在GPT-2中词表大小是50257; 为了加速并行对embedding的权重\(E_{H \times v}\) 按vocabulary的维度(也就是按列切分)进行拆分，结果 \(E=\left[ E_1, E_2 \right]， GEMM[Y1, Y2] = [XE_1, XE_2]\)，并行时通过all-gather通信得到最终结果：\(Y=all-gather([Y_1, Y_2])\), 然后再计算交叉熵的loss陨失，通信量是【batch-size x sequence-length x vocabulary-size】，这里vocabulary-size往往过大造成通信代价大。为了降低通信量，将 GEMM[Y1, Y2] 和 cross entropy loss进行fuse融合，可以降低通信量到 【batch-size x sequence-length】。

3. 参考