MOE论文详解(2)-GShard:Scaling Giant Models with Conditional Computation and Automatic Sharding
1. 背景说明
GShard是Google在2020年的一篇论文, 将 \(Sparsely\ Gated\ Mixture\ of\ Experts\) 与 transformer结合, 支持了600B大小的参数量, 使用了2048块TPU v3训练了4天翻译任务(100种语言翻译为英文).
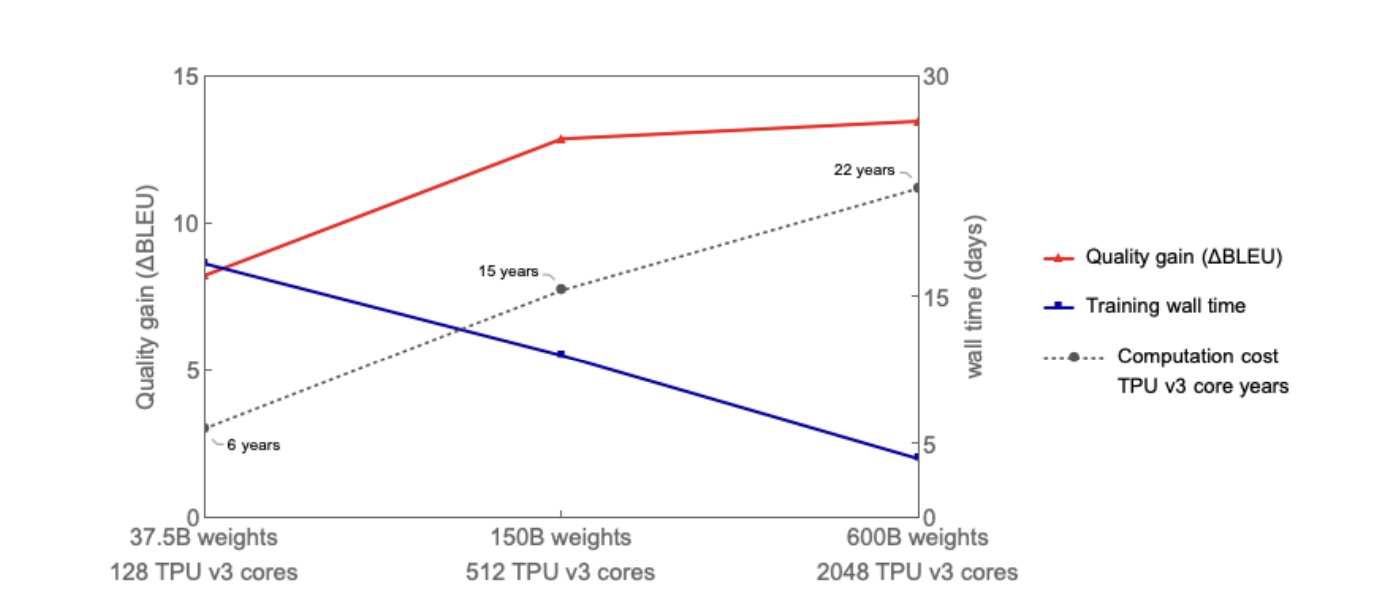
先看图中效果, 当参数量从37.5B增加到600B时, 模型效果(红色)越来越好, 计算耗时(点线)从6years到22years; 参数量大小增加了16x倍, 但训练成本只增加了3.6x倍; 这里训练wall-time(蓝色)是指的处理等量token所需要的时间也是接近线性下降;
论文中一些高效训练的思路:
- 亚线性扩展: 跟模型参数量相比, 算力和通信的需求增长要小于线性增长.
这点可以通过
Position-wise Sparsely Gated Mixture-of-Experts (MoE) layer来实现. - 训练抽象: 模型的定义与实际的分布式训练的切分和优化进行分离.
模型开发者只用关注具体的模型结构, 不用关心训练的具体实现,
对于模型开发者来说只用把集群当成一个具有大量memory和算力的单设备来使用就行.
为此提出了
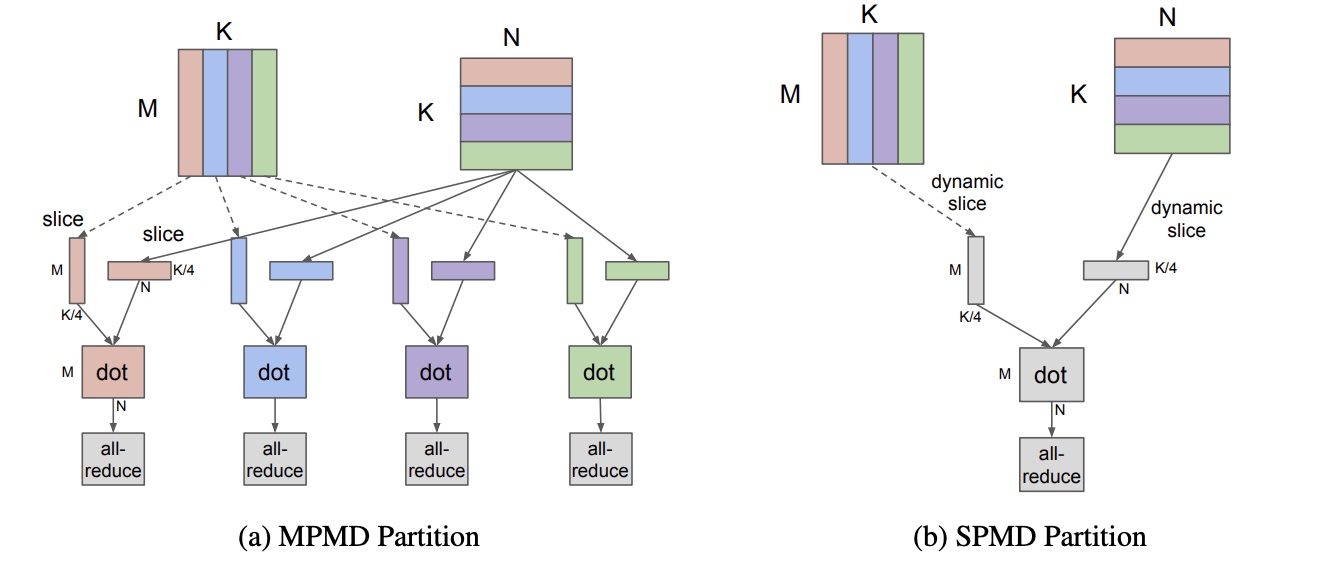
GShard的概念, 只用对一些关键的tensor进行切分策略的标注, 这里包括了一些注释的api定义与XLA中的编译扩展. - 编译可扩展: 系统要能方便支持成千上万台机器的并行计算扩展. 以4个结点的矩阵计算为例( \([M, K] \times [K, N] = [M, N]\) ), 计算两个矩阵相乘通常运行要使用如下图中的MPMD(多程序多数据)的方式计算, 手动把矩阵拆为4块, 每个结点读取对应矩阵块进行计算(写到代码中对应的程序读取的偏移不一样, 也就算成多个程序); 而这里论文中开发了一种SPMD(单程序多数据)的方式, 所有设备运行相同的程序,
2. 模型说明
2.1 Transformer架构的稀疏扩展
在 \(Transformer\) 的 \(Encoder\) 与 \(Decoder\) 中使用 \(top2-gating\) 的 \(MoE\ layer\) 进行稀疏扩展.
每条训练样本是通过一串由subword token的序列组成,
每个token会激活一部分MoE中的专家进行处理.
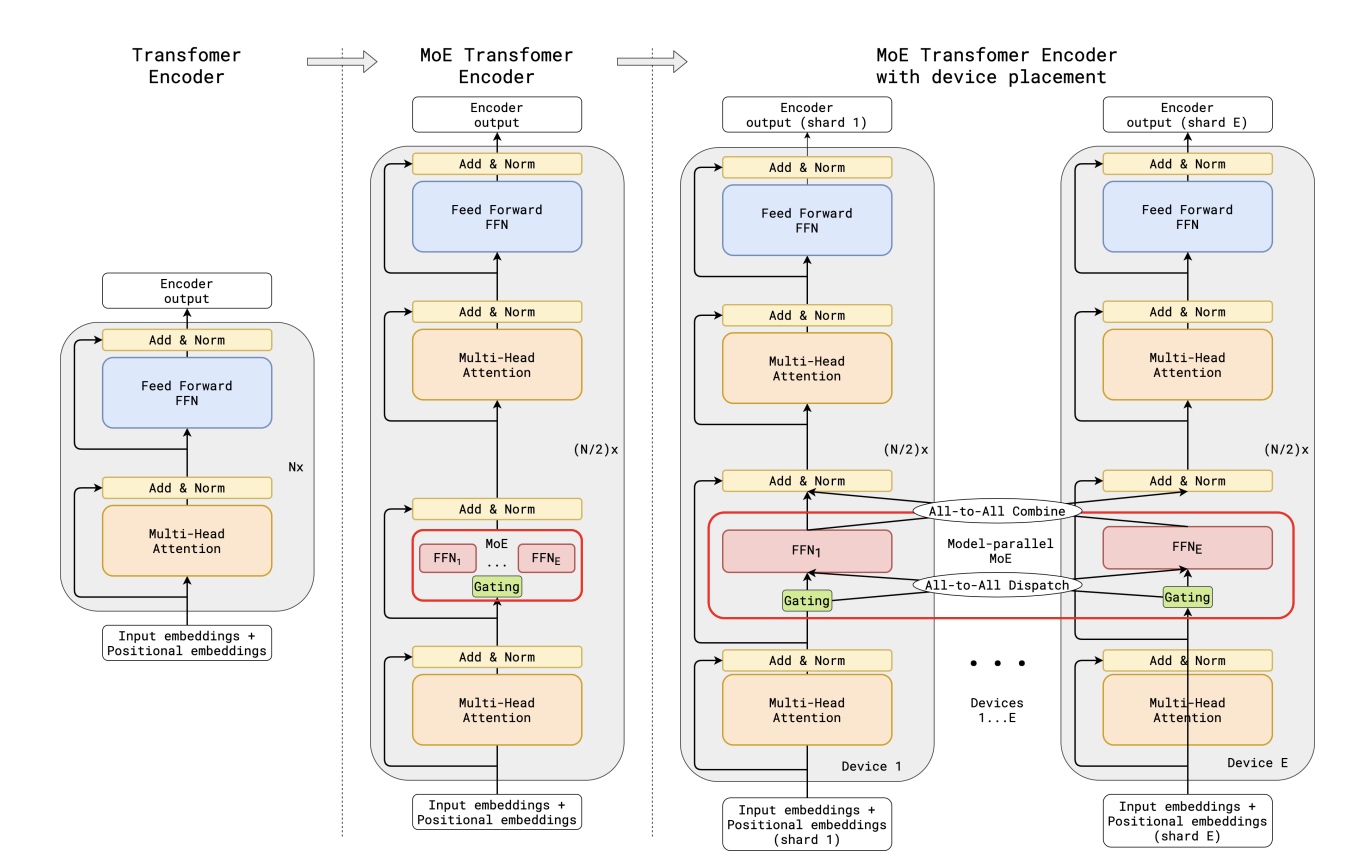 如图所示:
(a)以标准Transformer模型的编码器为例, 解码器结构类似
(b)通过用MoE层替换每个其他前馈层,我们得到了MoE
Transformer编码器的模型结构。
(c)当扩展到多个设备时,MoE层在多设备之间进行分片处理,除MoE层外的所有其他层都被复制。
如图所示:
(a)以标准Transformer模型的编码器为例, 解码器结构类似
(b)通过用MoE层替换每个其他前馈层,我们得到了MoE
Transformer编码器的模型结构。
(c)当扩展到多个设备时,MoE层在多设备之间进行分片处理,除MoE层外的所有其他层都被复制。
2.2 位置感知的MoE层(Position-wise Mixture-of-Experts Layer)
MoE
layer同样借鉴了The sparsely-gated mixture-of-experts layer论文中稀疏门控函数与辅助损失函数,
transformer中MoE layer由 \(E\) 个 \(FFN\) 网络组成, 每个 \(FFN\) 是一个专家, 基本定义如下(\(GATE\)):
\[\begin{gather} \mathcal{G}_{s, E} = GATE(x_s) \\ FFN_e(x_s) = wo_e \cdot ReLU(wi_e \cdot x_s) \\ y_s = \sum_{e=1}^{E} \mathcal{G}_{s,e} \cdot FFN_e(x_s) \\ \end{gather}\]
\(x_s\) 是MoE layer的输入token; \(wi_e\) 与 \(wo_e\) 分别是FFN网络输入与输出的weight权重, 用于输入与输出的映射; 向量 \(\mathcal{G}_{s, E}\) 是门控网络, 每个expert对应一个值, 值为0表示不会被分配token; 这里每个token最多会被分配给两个expert; 每个 \(FFN\) 是由两层全连接网络加上 \(ReLU\) 组成; 结果 \(y_s\) 由所有被选择expert输出的加权和组成.
\(GATE(\cdot)\) 决定了处理token的专家权重, 要满足两个要求: (1)均匀加载token, 不能让有的专家忙死, 有的专家饿死, 一个好的门控函数会均匀分配所有的token. (2) 并行扩展能够高效, 对于一个batch中有 \(N\) 个token, 由 \(E\) 个专家进行处理, 门控函数的开销为 \(O(NE)\), \(N\) 大小是million十亿级别, \(E\) 大小是千级别, 线性实现的门控网络会让大部分计算资源闲置.
为此给 \(GATE(\cdot)\) 设计了如下的机制:
- 专家容量(
Expert capacity). 为了专家处理的负载均衡, 为每个专家强制设置了固定处理的token数量, 也就是专家容量. 对于一个batch中有 \(N\) 个token, 有 \(E\) 个专家一起进行处理, 每个token会被发给最多两个专家, 专家容量为 \(O(N/E)\) . \(GATE(\cdot)\) 门控函数为每个专家 \(e\) 保存了一个计数器 \(c_e\) 来保存这个专家处理过的token数量. 如果要处理的token数量超过了这个专家的容量的话, 这个token被称为溢出(overflowed)token, 对应的 \(\mathcal{G}_{s, E}\) 会被设为全0向量, 这个token会通过残差连接直接传到下一个layer. - 局部分组分发(
Local group dispatching). \(GATE(\cdot)\) 会将所有训练中的token分为 \(G\) 组, 每组会包含有 \(S=N/G\) 个token, 每组会被相互独立来进行并行. 每个专家的容量会被设为 \(2N/(G \cdot E)\) , 这里2倍是一个容量系数. - 辅助损失(
Auxiliary loss). 总的loss函数设计为 \(\mathcal{L} = \mathcal{l}_{nll}+ k * \mathcal{l}_{aux}\),nll代表negative log likelihood,k是一个常数系数. 完整定义如下, 其中 \(c_e/S\) 表示input token分配给第 \(e\) 个expert的token比例, 我们的目标是为了最小化 \(c_e/S\) 的均方, 也就是让专家更均匀的处理token(均方mean square常用于计算方差, 比如常见的还有MSE均方误差). 由于 \(c_e\) 是从top-2中选出来的, 不可微分, 所以在loss中使用每个专家的平均gate值来近似计算, 将 \((c_e/S)^2\) 替换为了 \(m_e(c_e/S)\) , 这样就可以进行梯度下降.
\[\begin{gather} \mathcal{l}_{aux} = \frac{1}{E} \sum_{e=1}^{E} \frac{c_e}{S} \cdot m_e \end{gather}\]
- 随机路由(
Random routing): 如果top-2中第2个专家的权重 \(g_2\) 很小, 那么可以简单忽略第2个专家, 以此可以节约专家整体的容量, 根据 \(g_2\) 有概率地选择使用第2个专家
整体的门控算法描述如下:

这里为了方便对于top-2的计算拆成了两个for循环, 实际中可以合并成一个, 这样 \(top_2(g_s, E)\) 只用计算一遍, 对于top1的专家只用通过判断 \(c_{e1} < C\) 才选择第一个专家, 对于第2个专家的选择增加了随机的因素, 跟 \(2 \cdot g2\) 成正比, 如果第2个专家的权重越大, 那么选择上的概率越大.
如果只关注MoE模型的话到此就结束了, 后面是工程化的优化实现.
3. 使用GShard高效并行计算
这个章节中会有三个步骤, 首先使用将MoE模型表达为线性代数运算, 其次使用sharding的标注方式来对线性代数运算进行并行化, 最后编译器会接收一个(部分)注释的线性代数计算,并生成一个高效的并行程序,该程序可以扩展到数千个设备。
3.1 MoE模型的线性代数表示
首先给出MoE layer前向计算的过程,
算法2结合了爱因斯坦式(Einstein summation
notation)表示了一个单设备程度的执行过程. 具体说明如下:
- 门控函数被表示为一个einsum式加上一个softmax函数
- input token被分发给选择的expert被表示为一个einsum式,
结合了分发掩码(
dispatch_mask)和输入 - 所有的专家权重( \(FFN_e\) ) 被表示为3维向量 \(wi\) 与 \(wo\), 所有的专家网络(\(FFN_1 ...FFN_E\))的计算被表示为3个操作(两个einsum式与一个relu激活)
- 最后取所有专家输出的加权和使用另外一个einsum式来计算
 变量说明:
变量说明:
- G表示token的分组
- S表示输入token
- E表示expert专家
- C表示expert专家容量buffer中的位置
- M和H表示矩阵运算中向量化权重维度
- 图中标红的G与E表示tensor在分布式并行时向量会被切分
算法2中的Top2Gating函数用于计算局部分组的专家权重 \(\mathcal{G}_{S,E}\);
返回的combine_weights是一个4维向量,
shape大小为[G, S, E, C],
combine_weights[g, s, e, c] 的值不为0时,
表示一个在分组为g中的输入token
s被发送给了专家e,
并存储在专家e内缓存数组的第c个位置.
由于每一个token最多选top-2的专家进行分发,
所以在combine_weight[g, s, :, :]的切片中最多有两个非零值.
dispatch_mask是从combine_weights中得来的,
对于combine_weights中非零的位置全置为1做为掩码.
这里也初步计算了下训练计算复杂度( \(FLOPS\) )与设备个数( \(D\) )之间的关系, 先说结论: \(FLOPS/D=O(1)\) , 也就是随着并行设备的增加计算量是成接近线性的比例进行增长. 具体推算基于假设:
- 每个设备上token数 \(\frac{N}{D}=O(1)\);
- \(G=O(D), S=O(1), N=O(GS)=O(D)\);
- \(M = O(1), H = O(1)\);
- \(E = O(D)\);
- \(C = O(\frac{2S}{E})=O(\frac{1}{D}), D<S\);
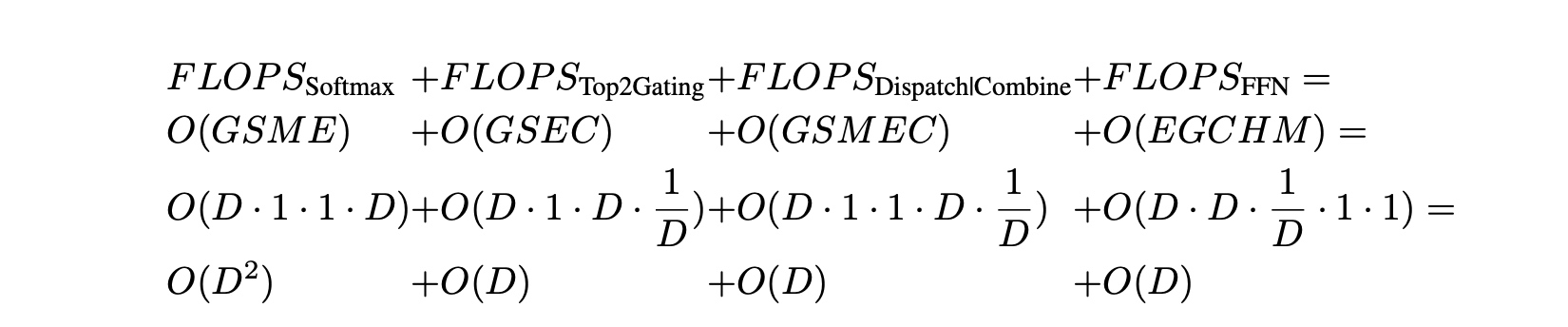 得到的最终每个device上的FLOPS量等于 \(FLOPS/D=O(D)+O(1)+O(1)+O(1)\), 虽然 \(FLOPS_{Softmax}\) 的复杂度是 \(O{D}\), 但 $ D H, D < S$, 可以看成是
\(O(1)\). 另外对于通信开销来说,
当设备数增长 \(D\), 对应通信开销按
\(O(\sqrt{D})\) 来增长.
得到的最终每个device上的FLOPS量等于 \(FLOPS/D=O(D)+O(1)+O(1)+O(1)\), 虽然 \(FLOPS_{Softmax}\) 的复杂度是 \(O{D}\), 但 $ D H, D < S$, 可以看成是
\(O(1)\). 另外对于通信开销来说,
当设备数增长 \(D\), 对应通信开销按
\(O(\sqrt{D})\) 来增长.
3.2 GShard的并行API说明(GShard Annotation API for Parallel Execution)
GShard中使用分块(sharding)API来对分布式中tensor如何切分进行描述, 切分信息会被传给编译器来实现并行执行的编译转换. 这里使用的API有三种:
replicate(tensor): 标注tensor会在不同的设备上进行复制权重. 通常应用到模型中的非MoE层的权重.split(tensor, split_dimension, num_partitions): 标注tensor会在第split_dimension个维度上切分为num_partitions份. 第i份切分会被放到第i个设备上,num_partitions不能超过所有的设备数shard(tensor, device_assignment): 生成多个split()操作, 从而支持多维度上的切分和设备分发, 而split只支持在单个维度上的数据切分. 一个3维tensor的shape是[3, 16, 64], device_assignment的shape大小是[1, 2, 4], device_assignment的内容是具体设备名, 那么切分后tensor的shape则为[3, 8, 16].- 有一个8卡的device, 想将一个[4, 8]的tensor分割成8个[2, 2]的tensor, 每个device上放一个切分后的tensor, 示例如下:
基于之前算法2的描述, 使用GShard的并行API进行改写, 使用1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
[["rank:0/cuda:0", "rank:0/cuda:1", "rank:0/cuda:2", "rank:0/cuda:3"],
["rank:1/cuda:4", "rank:1/cuda:5", "rank:1/cuda:6", "rank:1/cuda:7"],]split沿G的维度进行切片; 使用replicate对门控权重进行复制; 分发input时使用split沿E维度进行切片.
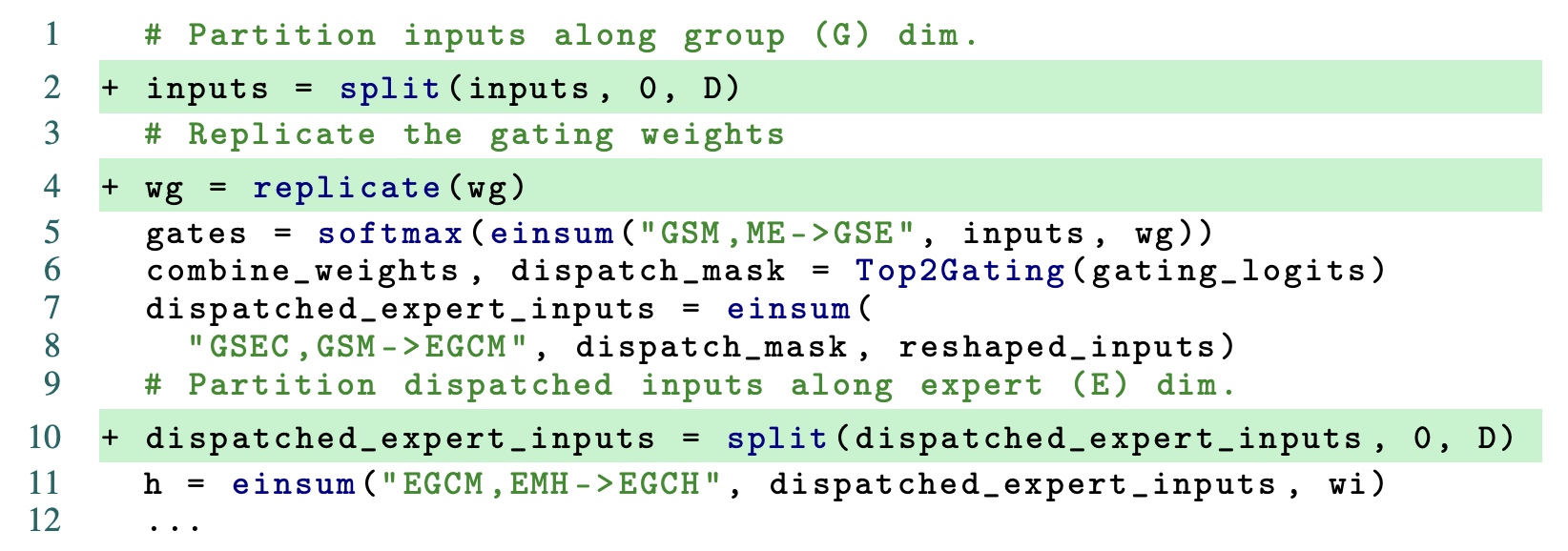
- 针对每个张量tensor进行切分: 在使用 GShard 进行模型切分时,我们不需要对程序中的每一个张量进行注解。通常只需要对一些重要的操作符,如上述示例中的 Einsum,进行注解(比如上图中标绿的split部分)。然后编译器会使用自己的启发式方法来推断其余张量的切分策略(比如上图中replicate部分)。
- 混合手动切分与自动切分: GShard 提供了使用分片注解的自动分区功能,这对于常见的情况已经足够了。但是,GShard 也有足够的灵活性,允许手动分区操作符与自动分区操作符混合使用。例如,假设你有一个大型数组,需要根据一个索引数组来选择元素。在这个过程中,你可能知道索引数组只会访问原始数组的一部分,比如前1000个元素。然而,当你使用 TensorFlow 或 XLA 的 Gather 操作符时,这个操作符并不知道这个信息。它会默认索引数组可能访问原始数组的任何位置,因此会在所有设备之间共享整个原始数组。这将导致大量不必要的数据通信,降低计算性能。你可以在每个设备上分别进行 Gather 操作,只访问该设备上的数组部分。这样,你就可以避免不必要的数据通信,提高计算性能。
在算法2中对于使用one-hot的mask矩阵进行输入的分发,
可以通过Gatehr操作来实现, 示例如下,
图中auto_to_manual_spmd_partition是进行手动的切分,
结合gather操作完成操作.

3.3 GShard的XLA SPMD分区器(The XLA SPMD Partitioner for GShard)
3.3.1 XLA通信原语
所有device运行相同程序, XLA中定义了类MPI的通信原语, 在SPMD分区器中常用的有如下几个:
- CollectivePermute: 操作符指定了一组源-目标对,源的输入数据被发送到相应的目标。它在两个地方被使用:改变一个分片张量在分区中的设备顺序,以及作为这一部分稍后讨论的 halo 交换。
- AllGather: 沿某一个维度下所有分区中的tensor进行concat操作, 每个device上从一个分片的tensor得到一个完全一样的大tensor
- AllReduce: 从所有分区上对tensor做sum操作
- AllToAll: 沿某一个维度在device上对tensor先进行切分, 然后发送到对应tensor上; 相当于对tensor进行了转置操作.
3.3.2 单操作符的SPMD的分区
Einsum式在用XLA HLO实现MoE模型中被当作了点(Dot)操作,
它的左操作符LHS和右操作符RHS都由三种维度组成:
- batch维度(Batch dimensions): 用于并行切分, 这个维度在输入输出中都必须存在
- 归约维度(Contracting dimensions): 用于归约计算, 只在输入中有, 在输出中会被归约计算省掉.
- 非归约维度(Non-Contracting dimensions): 在输入输出中都一直存在, 计算过程中也会保留
在sharding过程中优先基于batch维度来进行, 这样会避免跨分区的通信操作, 但实际中还是会存在跨分区的情况, 举了3种情况:
- 重新分区(Resharding): 专家分配的过程中需要对分区重新分配,
从group维度转为expert的维度, 适合用AllToAll来进行
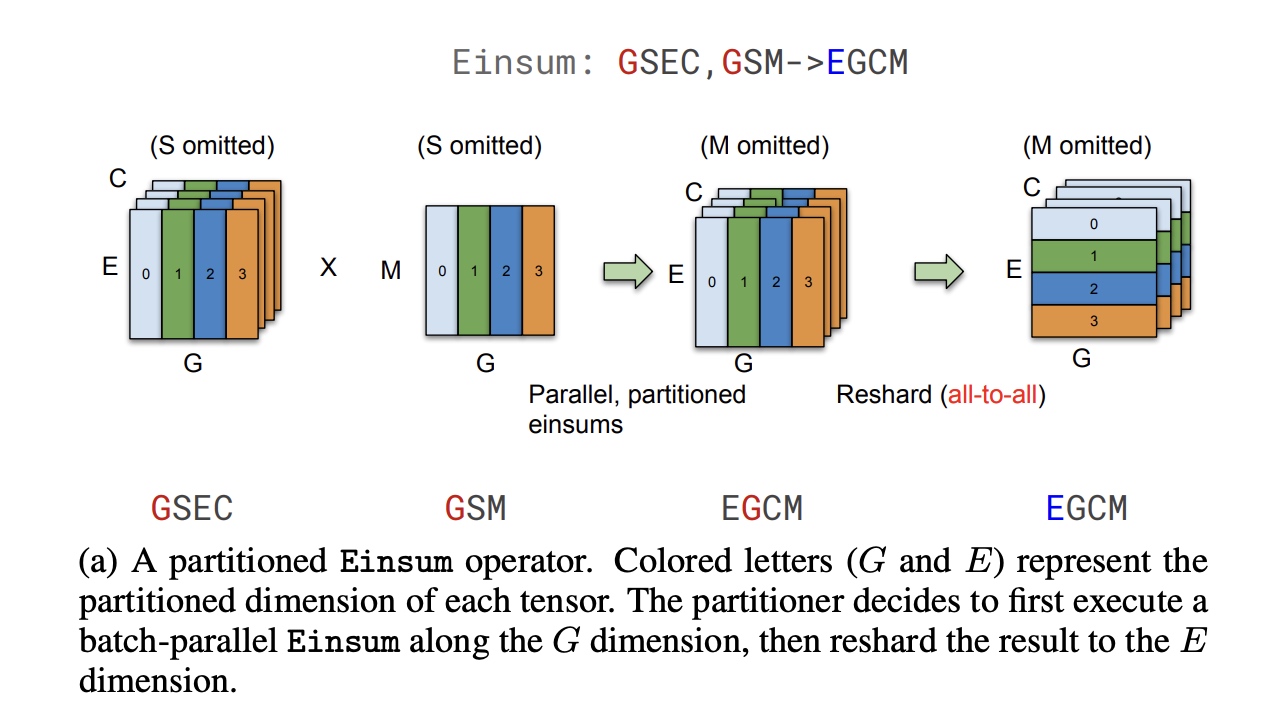
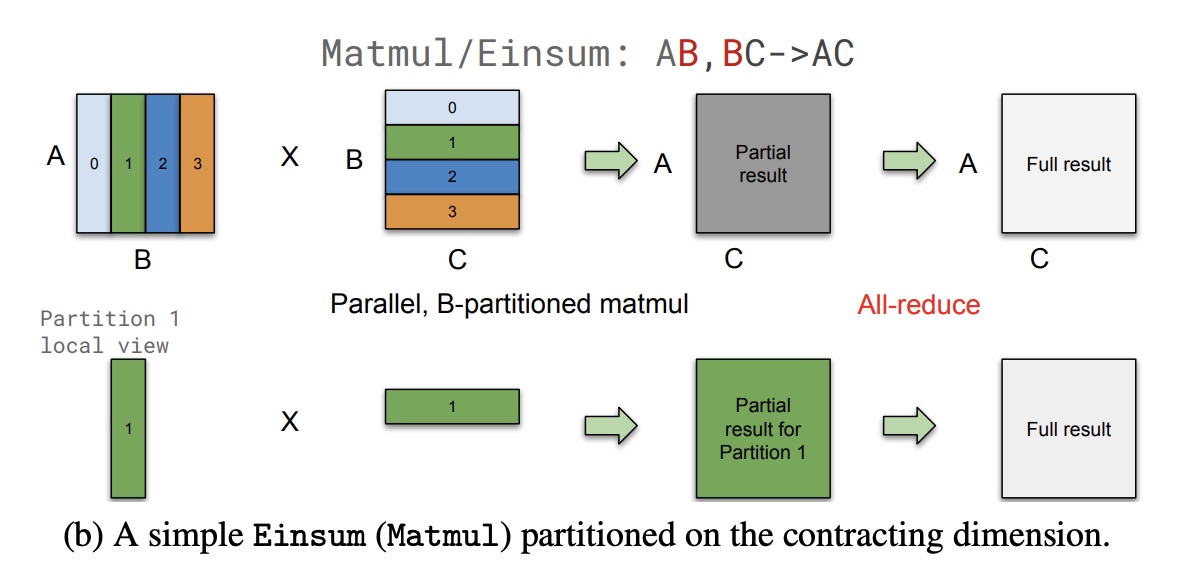
- 归约部分结果: 如果输入是按归约维度进行的切分,
那么我们会使用AllReduce来进行合并, 得到最终结果
- 循环切分: 对于特殊场景下为了避免每个分区中tensor大小过大,
在计算过程中保持分区的维度, 同时通过loop循环每次计算结果中的部分结果,
使用
CollectivePermute去通信调整输出的slice.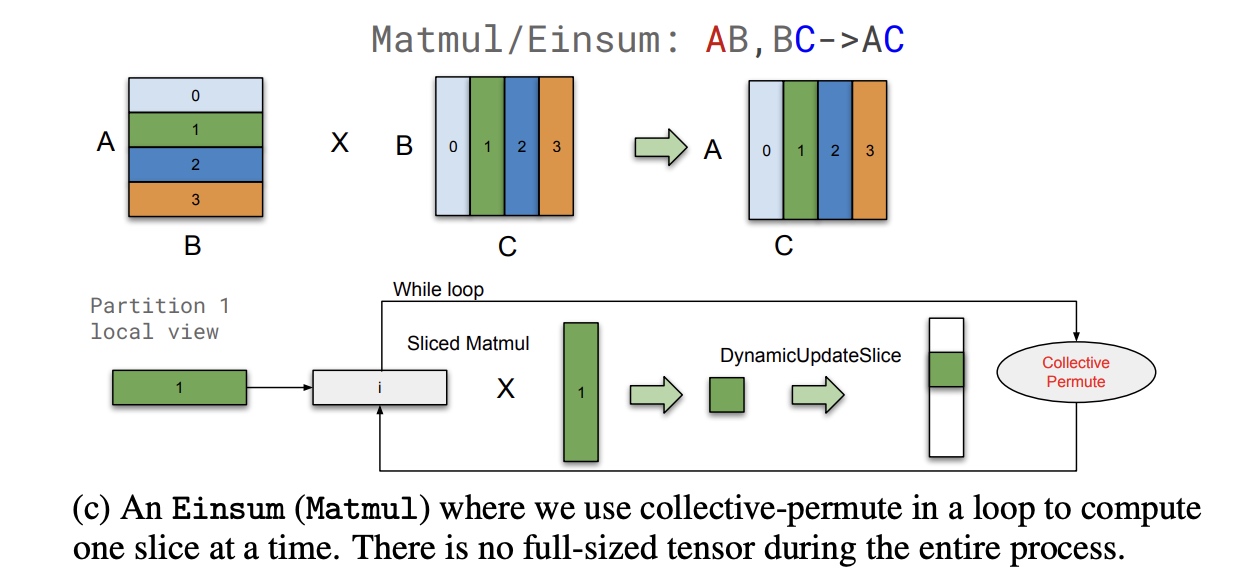
3.3.3 支持完备的操作符(Supporting a Complete Set of Operators)
上述过程中没有对tensor shape和操作符配置等进行过调整, 实际场景中会存在更复杂的情况:
静态shape和不均匀分区: XLA要求tensor shape是静态不变的, 但实际中有可能分区的大小不能被整除, 所以需要用到padding方法进行补齐. 假设我们有一个操作符需要处理的维度为15,并且我们希望将其划分为2个分区。由于15不能被2整除,划分后的每个分区会包含8个元素,而第一个分区会多出1个元素。使用Iota操作符生成一个范围为[0, 8)的序列,这个序列表示当前分区内的索引。计算每个分区的偏移量(PartitionId × 8), 跟全shape的索引进行比较, 偏移量小于15,则选择操作数的对应值, 否则选0
操作符配置: 在 XLA(加速线性代数)的上下文中,操作符确实具有静态配置,这些配置定义了它们在执行过程中的行为。这些配置包括填充、步幅和扩张等参数,这些参数在卷积等操作中至关重要。 最左边的分区可能在其左侧应用填充,而最右边的分区则在其右侧应用填充。这种差异源于数据的分区方式以及在分布式环境中如何处理边界。
Halo exchange: Halo exchange是一种常见的并行计算模式,特别是在处理网格或矩阵数据时。每个计算节点只处理数据的一个子集,但这些子集的边界(称为 “halo” 或 “ghost cells”)需要与邻居节点交换,以确保计算的一致性和正确性。
- 一种常见的
halo exchange的case是涉及窗口的操作符(像Convolution, ReduceWindow等)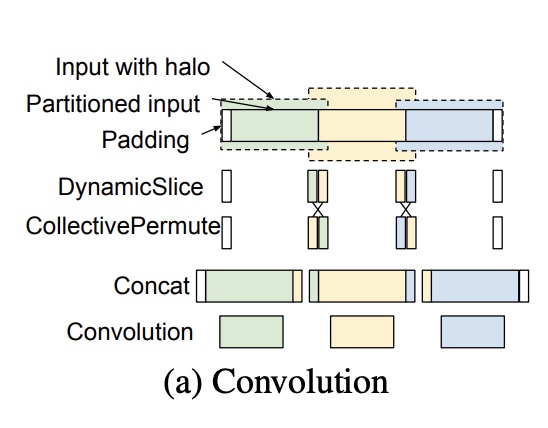
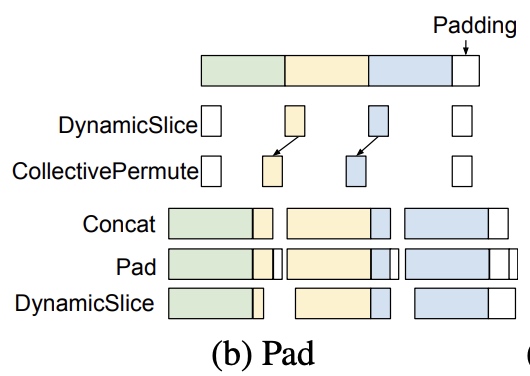
- 另外一种case是数据格式操作算子, 像Slice/Pad算子,
padding后tensor形状发生了变化, 需要重新考虑分区
- 还有一种格式操作算子, 虽不改变tensor的形状,
但不是需要用到
halo exchange, 例如使用Reverse算子改变了数据的排列顺序, 同时数据不能被分区整除, 这时就要使用padding来进行结果的补充; 还有例如使用Reshape算子, tensor从[3, 2] reshape为[6], 在第一个维度上3无法被2的分区整除, 但结果6是可以整除, 输入需要padding, 输出不用padding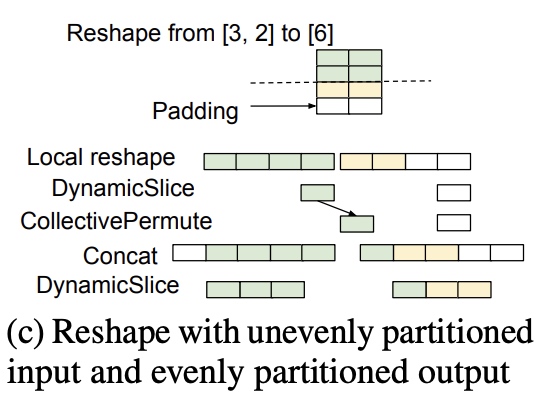
- 一种常见的